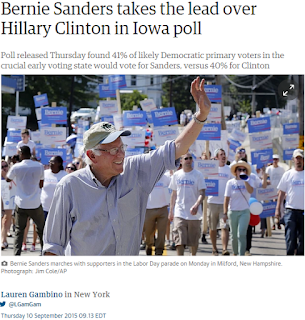
This headline is a good example of a) journalists misrepresenting statistics as well as b) confidence intervals/margin of error more broadly. See the headline below:
In actuality, Bernie didn't exactly take the lead over Hillary Clinton. Instead, a Quinnipiac poll showed that 41% of likely Democratic primary voters in Iowa indicated that they would vote for Sanders, while 40% reported that they would vote for Clinton.
If you go to the original Quinnipiac poll, you can read that the actual data has a margin of error of +/- 3.4%, which means that the candidates are running neck and neck. Which, I think, would have still been a compelling headline.
I used this as an example just last week to explain applied confidence intervals. I also used this as a round-about way of explaining how confidence intervals are now being used as an alternative/compliment to p-values.

Comments
Post a Comment